A Series of Fourier Transform Excercise

\section{Question 1}

Find the Fourier transform of the following signal. (Hint: make good use of the $\Lambda(\cdot)$ function)

\begin{figure}[h]
\centering

Rendered by QuickLaTeX.com

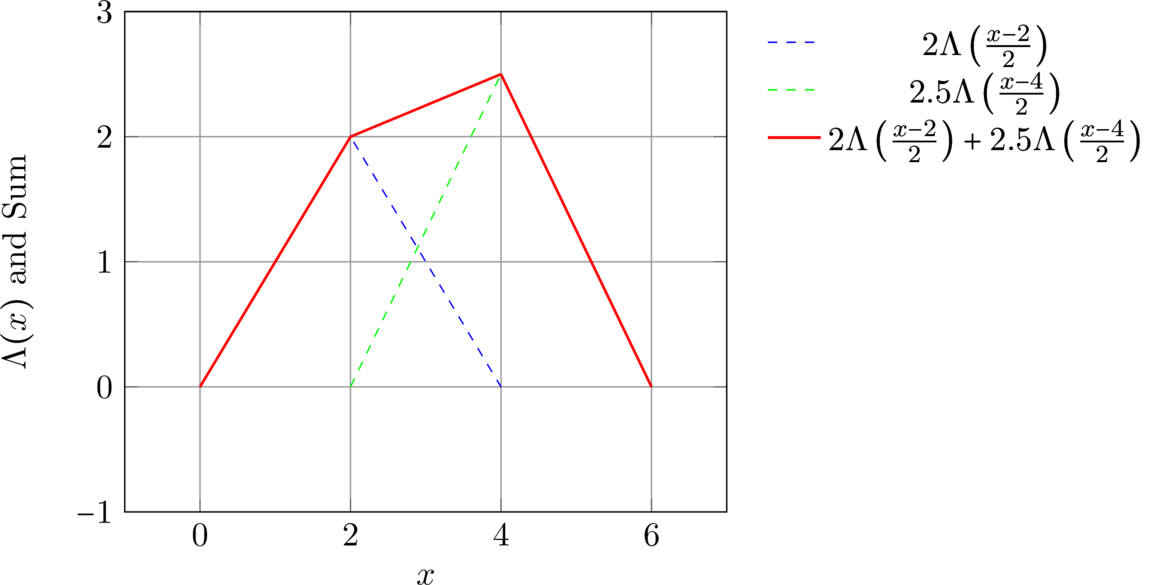
\caption{Time-domain representation of the signal in Question 1.}
\end{figure}

\textbf{Answer: }

We commence our investigation by deriving the Fourier transform of the scaled function $\Lambda\left(\frac{x}{c}\right)$ .

(1) $\begin{align*} \mathcal{F}\left(\Lambda\left(\frac{x}{c}\right)\right) &= \int_{-c}^{c} \Lambda\left(\frac{x}{c}\right) e^{-i 2 \pi s x} dx, \\ \intertext{By letting $\frac{x}{c} = y$, we obtain $x = cy$, which allows us to rewrite the integral as follows:} \mathcal{F}\left(\Lambda(y)\right) &= \int_{-1}^{1} \Lambda(y) e^{-i 2 \pi (s c) y} d(cy), \label{eq:substituted} \\ &= c \hat{f}(cs) \notag \\ &= c \mathbf{sinc}^2(cs). \label{eq:final} \end{align*}$

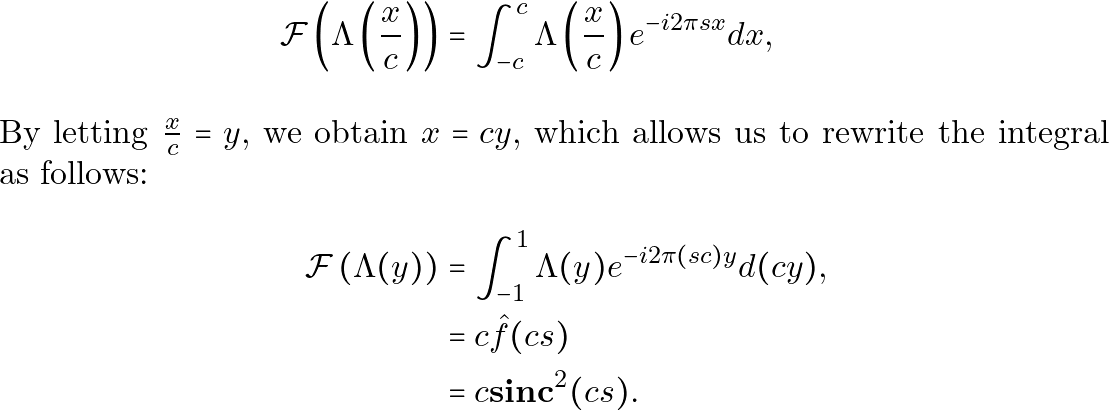
Leveraging the shift relation in Fourier transform,

$g(t-b) \xleftrightarrow{} e^{-j 2 \pi b s} G(s),$

we can extend the derivation to a generalized form for $a\Lambda\left(\frac{x-b}{c}\right)$ :

$\mathcal{F}\left(a\Lambda\left(\frac{x-b}{c}\right)\right) = a c \, e^{-j 2 \pi b s} \mathbf{sinc}^2(cs).$

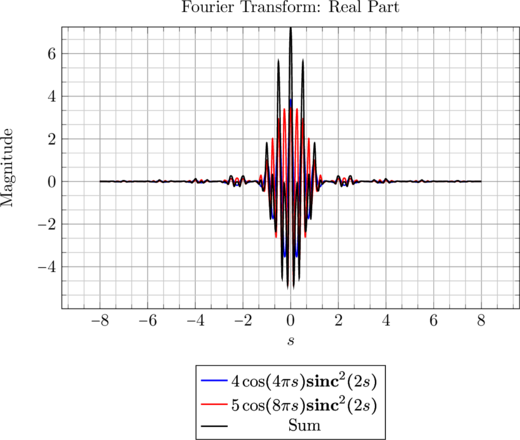
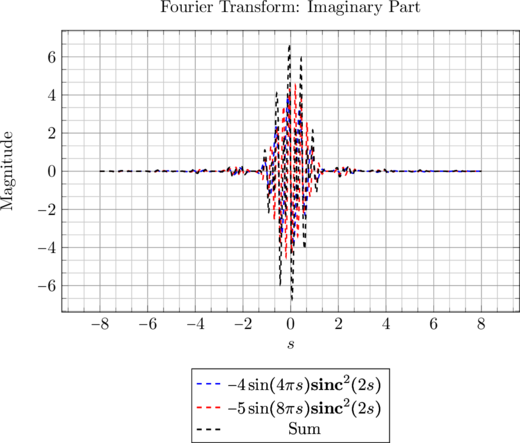
Thus, employing this generalized form, we deduce that (\Cref{fig:fourier_transform_2D})

$\mathcal{F}\left(2\Lambda\left(\frac{x-2}{2}\right) + 2.5\Lambda\left(\frac{x-4}{2}\right)\right) = 4 e^{-j 4 \pi s} \mathbf{sinc}^2(2s) + 5 e^{-j 8 \pi s} \mathbf{sinc}^2(2s).$

\begin{figure}[h]
\centering
\hbox{

Rendered by QuickLaTeX.com

\hspace{1cm}

Rendered by QuickLaTeX.com

}
\caption{Fourier Transform of $4 e^{-j 4 \pi s} \mathbf{sinc}^2(2s) + 5 e^{-j 8 \pi s} \mathbf{sinc}^2(2s)$ : Real and Imaginary Parts}
\label{fig:fourier_transform_2D}
\end{figure}

发表评论 取消回复

发表评论取消回复