Table of Contents
This tutorial provides a complete, step-by-step derivation of the Lorentz force law starting from the Lagrangian. The tutorial includes the derivation of key vector identities and explicitly details each term involved in the process. The goal is to make the content understandable even for someone new to the subject.
Step 1: Define the Lagrangian 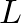
The Lagrangian ![]() is a function that describes the dynamics of a system. For a charged particle of mass
is a function that describes the dynamics of a system. For a charged particle of mass ![]() and charge
and charge ![]() moving in electromagnetic fields described by a vector potential
moving in electromagnetic fields described by a vector potential ![]() and a scalar potential
and a scalar potential ![]() , the Lagrangian
, the Lagrangian ![]() is defined as:
is defined as:
![Rendered by QuickLaTeX.com \[L = \frac{1}{2}m\vec{\dot{x}} \cdot \vec{\dot{x}} + q\vec{\dot{x}} \cdot \vec{A} - q\phi\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-e9396de65a98254e91385848e55648b1_l3.png)
Here, ![]() is the velocity of the particle, and the dot represents a time derivative.
is the velocity of the particle, and the dot represents a time derivative.
Step 2: Compute 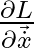
To proceed, we need to find the partial derivative of ![]() with respect to
with respect to ![]() . This derivative is obtained as follows:
. This derivative is obtained as follows:
![Rendered by QuickLaTeX.com \[\frac{\partial L}{\partial \vec{\dot{x}}} = m\vec{\dot{x}} + q\vec{A}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-58d404ab61cd18605f83527d338390cd_l3.png)
Step 3: Derive the Vector Identity
Before diving into the next steps, let’s derive a key vector identity that will be used later. The identity is:
![]()
The derivation of this identity involves using the definitions of gradient, divergence, and curl, along with the product rule for derivatives. Due to its complexity, it’s typically proven using tensor notation or by working through each Cartesian component.
Step 4: Compute 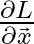 with Explicit Derivation of Terms
with Explicit Derivation of Terms
Now, we’ll find the partial derivative of ![]() with respect to
with respect to ![]() . This involves differentiating the terms
. This involves differentiating the terms ![]() and
and ![]() .
.
Derivation of the 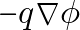 Term
Term
The ![]() term differentiates to
term differentiates to ![]() when taking the gradient with respect to
when taking the gradient with respect to ![]() .
.
Derivation of the Last Two Terms from 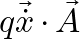
Using the vector identity derived in Step 3, the gradient of ![]() becomes:
becomes:
![]()
These two terms will be part of ![]() .
.
Final Expression for 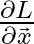
Combining these terms, we get:
![Rendered by QuickLaTeX.com \[\frac{\partial L}{\partial \vec{x}} = -q \nabla \phi + q (\vec{\dot{x}} \cdot \nabla) \vec{A} + q \vec{\dot{x}} \times (\nabla \times \vec{A})\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-44bdbf54ec426d8247d930c329989931_l3.png)
Step 5: Euler-Lagrange Equation and Time Derivative
The Euler-Lagrange equation states:
![Rendered by QuickLaTeX.com \[\frac{d}{dt} \left( \frac{\partial L}{\partial \vec{\dot{x}}} \right) - \frac{\partial L}{\partial \vec{x}} = 0\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-65f99217d2b0cf7ea83a39dab1aba883_l3.png)
To apply this equation, we need to find the time derivative of ![]() , which is:
, which is:
![Rendered by QuickLaTeX.com \[\frac{d}{dt}(m\vec{\dot{x}} + q\vec{A}) = m\vec{\ddot{x}} + q\frac{d\vec{A}}{dt}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-d82a9cfd955077ddff543c543fb2cd50_l3.png)
The total time derivative ![]() includes both explicit and implicit time dependencies:
includes both explicit and implicit time dependencies:
![Rendered by QuickLaTeX.com \[\frac{d\vec{A}}{dt} = \frac{\partial \vec{A}}{\partial t} + (\vec{\dot{x}} \cdot \nabla) \vec{A}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-47061b41ef4d1862490e3d7653b4e70b_l3.png)
Step 6: Substitute into Euler-Lagrange Equation and Simplify
Having all the necessary derivatives and expressions at hand, we can now substitute these into the Euler-Lagrange equation:
![Rendered by QuickLaTeX.com \[\frac{d}{dt} \left( \frac{\partial L}{\partial \vec{\dot{x}}} \right) - \frac{\partial L}{\partial \vec{x}} = 0\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-65f99217d2b0cf7ea83a39dab1aba883_l3.png)
We had:
![Rendered by QuickLaTeX.com \[\frac{d}{dt}(m\vec{\dot{x}} + q\vec{A}) = m\vec{\ddot{x}} + q \left( \frac{\partial \vec{A}}{\partial t} + (\vec{\dot{x}} \cdot \nabla) \vec{A} \right)\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-b157b19eb8dae7239f2b28a4961c4eb4_l3.png)
And:
![Rendered by QuickLaTeX.com \[\frac{\partial L}{\partial \vec{x}} = -q \nabla \phi + q (\vec{\dot{x}} \cdot \nabla) \vec{A} + q \vec{\dot{x}} \times (\nabla \times \vec{A})\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-44bdbf54ec426d8247d930c329989931_l3.png)
Substituting these into the Euler-Lagrange equation, we get:
![Rendered by QuickLaTeX.com \[m\vec{\ddot{x}} + q \left( \frac{\partial \vec{A}}{\partial t} + (\vec{\dot{x}} \cdot \nabla) \vec{A} \right) = q \left( -\nabla \phi + (\vec{\dot{x}} \cdot \nabla) \vec{A} + \vec{\dot{x}} \times (\nabla \times \vec{A}) \right)\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-4e5928da693190ae39b41e212cae78f0_l3.png)
Simplifying, we find:
![Rendered by QuickLaTeX.com \[m\vec{\ddot{x}} = q \left( -\nabla \phi - \frac{\partial \vec{A}}{\partial t} \right) + q \vec{\dot{x}} \times (\nabla \times \vec{A})\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-d489e2907686246bda8efcef65e5f991_l3.png)
Finally, using ![]() and
and ![]() , we arrive at the Lorentz force law:
, we arrive at the Lorentz force law:
![]()
Conclusion
This concludes the comprehensive tutorial on deriving the Lorentz force law from the Lagrangian. The tutorial aimed to be as detailed as possible, explicitly showing the derivation of each term and equation involved. I hope you find this tutorial complete and informative.
SI
Derivation Using Limits
The Definition of the Total Derivative
The total derivative ![]() of a vector field
of a vector field ![]() is defined by the limit:
is defined by the limit:
![Rendered by QuickLaTeX.com \[\frac{d\vec{A}}{dt} = \lim_{{\Delta t \to 0}} \frac{\vec{A}(t + \Delta t, \vec{x}(t + \Delta t)) - \vec{A}(t, \vec{x}(t))}{\Delta t}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-ad6176c7ba7424c04ffd2d541c0e35c7_l3.png)
Breaking Down the Limit Expression
We can express ![]() using a Taylor series expansion around
using a Taylor series expansion around ![]() :
:
![Rendered by QuickLaTeX.com \[\vec{A}(t + \Delta t, \vec{x}(t + \Delta t)) \approx \vec{A}(t, \vec{x}(t)) + \Delta t \left( \frac{\partial \vec{A}}{\partial t} \right)_{\vec{x}(t)} + \Delta \vec{x} \cdot \left( \nabla \vec{A} \right)_{\vec{x}(t)}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-50dd44c1d36cb74d3fd647f02d683b07_l3.png)
where ![]() .
.
Factor Out 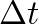
Now, we can substitute this expansion back into the limit expression for ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{d\vec{A}}{dt} = \lim_{{\Delta t \to 0}} \frac{ \vec{A}(t, \vec{x}(t)) + \Delta t \left( \frac{\partial \vec{A}}{\partial t} \right)_{\vec{x}(t)} + \Delta \vec{x} \cdot \left( \nabla \vec{A} \right)_{\vec{x}(t)} - \vec{A}(t, \vec{x}(t))}{\Delta t}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-80729453a63cf369e8e4c5ed24cc5a00_l3.png)
Factoring out ![]() in the numerator, we get:
in the numerator, we get:
![Rendered by QuickLaTeX.com \[\frac{d\vec{A}}{dt} = \lim_{{\Delta t \to 0}} \left( \frac{\partial \vec{A}}{\partial t} \right)_{\vec{x}(t)} + \frac{\Delta \vec{x}}{\Delta t} \cdot \left( \nabla \vec{A} \right)_{\vec{x}(t)}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-f6e5ae7a745cf1d79d273dab8e1919dc_l3.png)
Taking the Limit
As ![]() approaches zero,
approaches zero, ![]() approaches
approaches ![]() , the velocity of the particle. So, we have:
, the velocity of the particle. So, we have:
![Rendered by QuickLaTeX.com \[\frac{d\vec{A}}{dt} = \left( \frac{\partial \vec{A}}{\partial t} \right) + \vec{\dot{x}} \cdot \nabla \vec{A}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-7d141f62d0c2a417a6808d6dddf1c04b_l3.png)
This gives us the expression for the total time derivative ![]() , which includes both the explicit and implicit time dependencies.
, which includes both the explicit and implicit time dependencies.
Certainly, demonstrating the vector identity through a concrete 3D example can offer a tangible way to grasp its intricacies. The vector identity we’re interested in is:
![]()
For simplicity, let’s consider ![]() and
and ![]() as 3D vectors defined in Cartesian coordinates
as 3D vectors defined in Cartesian coordinates ![]() :
:
![]()
![]()
Tutorial: Verifying the Vector Identity in 3D
Step 1: Compute 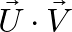
The dot product ![]() is given by:
is given by:
![]()
Step 2: Compute 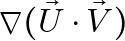
The gradient of ![]() with respect to
with respect to ![]() is:
is:
![Rendered by QuickLaTeX.com \[\nabla (\vec{U} \cdot \vec{V}) = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) \cdot (U_x V_x + U_y V_y + U_z V_z)\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-0a92e1ab8b7df5e78042fa904ecadca8_l3.png)
This results in a vector with components:
![Rendered by QuickLaTeX.com \[\left( \frac{\partial}{\partial x}(U_x V_x) + \frac{\partial}{\partial y}(U_y V_y) + \frac{\partial}{\partial z}(U_z V_z) \right) \hat{i} + \text{(similar terms for } \hat{j} \text{ and } \hat{k} \text{)}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-585e81a99cf5bda2db34a87b75fbe60e_l3.png)
Step 3: Compute 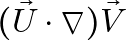 and
and 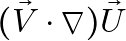
The term ![]() can be written as:
can be written as:
![Rendered by QuickLaTeX.com \[(U_x \frac{\partial}{\partial x} + U_y \frac{\partial}{\partial y} + U_z \frac{\partial}{\partial z}) \cdot (V_x \hat{i} + V_y \hat{j} + V_z \hat{k})\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-e7cdf8c1d3ce6257313a4f7d5612ef9e_l3.png)
After performing the dot product, we get:
![Rendered by QuickLaTeX.com \[U_x \frac{\partial V_x}{\partial x} \hat{i} + U_y \frac{\partial V_y}{\partial y} \hat{j} + U_z \frac{\partial V_z}{\partial z} \hat{k}\]](https://blog.lazying.art/wp-content/ql-cache/quicklatex.com-6c246a0a4729c0476942911c98651b8d_l3.png)
A similar calculation can be done for ![]() .
.
Step 4: Compute 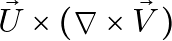 and
and 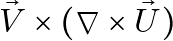
Computing the curl ![]() and
and ![]() yields vectors in
yields vectors in ![]() components. The cross product
components. The cross product ![]()
