Quantum Field Theory for the Gifted Amateur Exercise 1.5 Surfing the Quantum Waves

Welcome back, fellow aficionados of quantum mechanics! The journey through Quantum Field Theory for the Gifted Amateur has led us to yet another fascinating pitstop—Exercise 1.5. Today, we shall delve deep into the intricacies of three-dimensional elastic media and explore how they abide by the wave equation.

Table of Contents

## Setting the Stage: Elastic Media and Energies

To get started, let’s consider an elastic medium described by a scalar field $\psi(x, t)$ . This medium is characterized by two crucial energies: the potential energy $V$ and the kinetic energy $T$ :

$V = \frac{\mathcal{T}}{2} \int d^3x (\nabla \psi)^2$

$T = \frac{\rho}{2} \int d^3x \left( \frac{\partial \psi}{\partial t} \right)^2$

The mathematical forms look fancy, but they boil down to quantifying how much energy is stored or moving in the medium.

## The Lagrangian: The Soul of Classical Mechanics

The Lagrangian $L$ , a cornerstone concept in classical mechanics, is the difference between kinetic and potential energies:

$L = T - V$

## The Action: Where the Magic Happens

But physics, especially quantum mechanics, likes to go beyond the obvious. Here comes the Action $A$ , defined as the integral of the Lagrangian over time:

$A = \int (T - V) dt$

## The Equation of Motion: A Deep Dive into Functional Derivatives

### Definitions

First, recall the definitions of potential energy $V$ and kinetic energy $T$ :

$V = \frac{\mathcal{T}}{2} \int \mathrm{d}^3 x (\nabla \psi)^2$

$T = \frac{\rho}{2} \int \mathrm{d}^3 x \left(\frac{\partial \psi}{\partial t}\right)^2$

The action $A$ is defined as:

$A = \int (T - V) \mathrm{d}t$

### Functional Derivative

We aim to find the equation of motion by taking the functional derivative $\frac{\delta A}{\delta \psi}$ and setting it equal to zero. Consider a small variation in $\psi$ , $\epsilon \delta(x - x_0)$ , and find how $A$ changes:

$\begin{aligned} \frac{\delta A}{\delta \psi} = \lim_{\epsilon \to 0} \frac{1}{\epsilon} &\int \mathrm{d}t \int \mathrm{d}^3 x \Bigg\{ \frac{\rho}{2} \left(\frac{\partial (\psi + \epsilon \delta(x - x_0))}{\partial t}\right)^2 \\ &- \frac{\mathcal{T}}{2} (\nabla (\psi + \epsilon \delta(x - x_0)))^2 \\ &- \left[ \frac{\rho}{2} \left(\frac{\partial \psi}{\partial t}\right)^2 - \frac{\mathcal{T}}{2} (\nabla \psi)^2 \right] \Bigg\} \end{aligned}$

### Expansion and Simplification

Expanding the terms and collecting those that are proportional to $\epsilon$ , we get:

$\begin{aligned} \frac{\delta A}{\delta \psi} &= \lim_{\epsilon \to 0} \frac{1}{\epsilon} \int \mathrm{d}t \int \mathrm{d}^3 x \Bigg\{ \rho \frac{\partial \psi}{\partial t} \frac{\partial (\epsilon \delta(x - x_0))}{\partial t} \\ &- \mathcal{T} \nabla \psi \cdot \nabla (\epsilon \delta(x - x_0)) \Bigg\} \\ &= \int \mathrm{d}t \int \mathrm{d}^3 x \Bigg\{ -\mathcal{T} \nabla \psi \cdot \nabla \delta(x - x_0) + \rho \frac{\partial \psi}{\partial t} \frac{\partial \delta(x - x_0)}{\partial t} \Bigg\} \end{aligned}$

Setting $\frac{\delta A}{\delta \psi} = 0$ , we find:

$-\mathcal{T} \nabla^2 \psi + \rho \frac{\partial^2 \psi}{\partial t^2} = 0$

### Final Wave Equation

Finally, isolating $\psi$ to one side, we get the wave equation:

$\nabla^2 \psi = \frac{\rho}{\mathcal{T}} \frac{\partial^2 \psi}{\partial t^2}$

$\nabla^2 \psi = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2}$

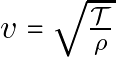where $v = \sqrt{\frac{\mathcal{T}}{\rho}}$ is the velocity of the wave.

And there you have it! Our field $\psi$ indeed obeys the wave equation, where $v$ stands for the wave velocity. Notice how the functional derivative effectively encapsulates the behavior of the field over time and space, bringing us to our desired wave equation.

Join us next time for more unraveling, decoding, and perhaps a few more “Eureka!” moments. Until then, may your quantum fields be ever undulating!

## Wrapping Up: The Unification of Dimensions

Today’s exercise allowed us not only to solve a fundamental problem in quantum mechanics but also to bridge the gap between 3D space and 4D spacetime. Isn’t it fascinating how all these equations and variables waltz seamlessly across dimensions?